Autor: Quinky

Grundsätzlich ist die Voraussetzung für die Durchführung der Regressionsanalyse, daß das Regressionsmodell korrekt spezifiziert ist. Wenn dies nicht der Fall ist, dann ist von vornherein keine Abhängigkeit zu erwarten oder gefundene Abhängigkeiten können Artefakte sein. Zur Aufstellung eines Regressionsmodells ist also eine umfangreiche Vorarbeit notwendig.

Bei allen oben dargestellten Modellen wird aufgrund der umfangreichen theoretischen Vorarbei­ten davon ausgegangen, daß sie korrekt spezifiziert sind. Dabei steht fest, wie schon am Anfang der Untersuchung ausgeführt wurde, daß ein Verhalten oder auch eine Ein­stellung von einer unübersehbar großen Anzahl von Faktoren beeinflußt wird. Diese konnten und sollten nicht alle Gegenstand dieser Untersuchung sein. „Eine vollständige Modell­formulierung setzt im Prinzip das Vorhandensein erschöpfenden theoretischen Wissens über den untersuchten Zusammenhang voraus. Dieses ist jedoch aus wissenschafts­theoretischen Überlegungen heraus prinzipiell niemals möglich, sodaß das Postulat der Vollständigkeit immer nur als Leitidee zu verstehen ist.“[1]

Auf der anderen Seite wird aufgrund der theoretischen Vorarbeiten davon ausgegangen, daß die Faktoren, die mit in das Modell einbezogen wurden, einen Erklärungsgehalt für dasselbe haben.

---

[1] Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R., (1994), S. 31

Die Anwendung der Kleinst-Quadrate-Schätzung im Rahmen der Regressionsanalyse, setzt sowohl für die abhängige, als auch für die unabhängigen Variablen metrisches Skalennivau voraus.

Die im Fragebogen hauptsächlich verwendeten Rating-Skalen können nicht grundsätzlich als Intervallskalen, also als metrische Skalen bezeichnet werden. Es ist jedoch üblich von diesen anzunehmen, sie seien intervallskaliert und sie dann auch entsprechend zu behandeln.[1] „Hinter dieser ‚liberalen‘ Auffassung steht die Überzeugung, daß die Bestätigung einer Forschungshy­pothese durch die Annahme eines falschen Skalenniveaus eher erschwert wird.“[2] Dies ist in dieser Untersuchung umso berechtigter, als durch Verbindung mehrerer Items, von denen einige Intervallskalenniveau haben, die Annahme der Intervallskalierung noch bestärkt wird.

Bei den folgenden Untersuchungen wird deshalb davon ausgegangen, daß die verwendeten Daten intervallskalliert sind.

---

[1] vgl.: Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. (1994), S. XIV

[2] Bortz, J., (1993), S. 27

Ein wichtiger Bestandteil der Regressionsanalyse sind die Residuen. Diese müssen eine ganze Reihe von Bedingungen erfüllen, damit die Schätzungen durch die Regressionsanalyse effizient sind.

Eine Prämisse des Regressionsmodells fordert, daß die Residuen, die ihre Ursache in den Störgrößen haben, nicht miteinander korrelieren. Wenn diese Prämisse nicht erfüllt ist, sprechen wir von Autokor­relation. Bei Zeitreihenanalysen gibt es eine sinnvolle Reihenfolge der Daten, wodurch zum Beispiel eine serielle Korrelation leicht nachgewiesen werden kann. Bei Querschnittsdaten ist die Reihenfolge der Fälle beliebig. „Das führt dazu, daß dort vorhandene Korrelationen kaum zu identifizieren sind.“[1] Aus diesem Grunde wird der Durbin/Watson-Test-Wert, der als Maßzahl der Autokorrelation üblich ist nicht berechnet. Dieser Test hat die Reihenfolge der Residuen der Beobachtungswerte zum Gegenstand der Analyse. Die Ausgangsdaten können aber durch Umstellung der Fälle beliebig geändert werden. Da die Reihenfolge der Eingabe der einzelnen Fälle rein zufällig erfolgte, hätte der Durbin/Watson-Test keine Aussagekraft. Es wird aus diesem Grunde angenommen, daß keine Autokorrelation besteht.

Eine weitere Voraussetzung des Regressionsmodells ist, daß die Varianz der Residuen homo­gen ist, das heißt, daß keine Heteroskedastizität vorliegt. Mit anderen Worten bedeutet dies, daß die Residualgröße nicht vom Betrag oder der Reihenfolge der Beobachtungen der unabhängigen Variablen beeinflußt werden darf.[2] Um diese Bedingung überprüfen zu können, eignen sich die standardisierten und studentisierten Residuen am besten.[3] Sowohl Backhaus[4], als auch Kockläuner[5] schlagen in erster Linie die Überprüfung dieser Bedingung mit Hilfe graphischer Hilfsmittel vor.

Wie oben schon ausgeführt, kann eine Abhängigkeit von der Reihenfolge der Beobachtungen ausgeschlossen werden. Zu überprüfen bleibt eine unter Umständen vorhandene Abhängigkeit vom Betrag. Die studentisierten Residuenwerte sind aufgrund ihrer Konstruktion mit den Vorhersagewerten leicht korreliert. Dies stört in diesem Fall jedoch nicht, da es nur darauf ankommt, daß die Residuenwerte mit konstanter Streuung zufällig um Null verteilt sind. Wenn sich in einem Streudiagramm eine abhängig von den Vorhersagewerten variierende Streuung der studentisierten Residuen findet, dann deutet das auf eine Verletzung der Annahme von Homoskedastizität hin.[6]

Sämtliche Diagramme zu den oben angegebenen Regressionen wurden überprüft. Keines der Streudiagramme läßt eine deutliche Abhängigkeit der Varianz von den Vorhersagewerten erkennen. Damit gilt die Bedingung der Homoskedastizität für alle Regressionsmodelle als erfüllt.

---

[1] Kockläuner, Gerhard, (1988), S. 70

[2] Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. (1994), S. 35

[3] vgl.: Kockläuner, Gerhard, (1988), S. 67

[4] vgl.: Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R., (1994), S. 35

[5] vgl.: Kockläuner, Gerhard, (1988), S. 67

[6] vgl.: Kockläuner, Gerhard, (1988), S. 67

Eine weitere Voraussetzung für die Anwendbarkeit des Regressionsmodells ist die Abwesen­heit von Multikollinearität zwischen den unabhängigen Variablen. Das bedeutet, daß sich ein Regressor nicht als Linearkombination der übrigen Regressoren darstellen lassen darf. Multikol­linearität wird erst dann zum Problem, wenn eine starke lineare Abhängigkeit zwischen den Regressoren besteht.[1] Bei zwei Regressoren reicht es aus, anhand der Korrelationsmatrix zu überprüfen, ob Korrelationen bestehen. Bei drei oder mehr Regressoren läßt sich dieses Krite­rium durch die Auswertung der Toleranzen der Regressoren klären. Diese berechnen sich aus: 1-Bestimmt­heitsmaß einer Regressionsanalyse aller unabhängigen Variablen mit der jeweils zu untersuchenden unabhängigen Variablen als Regressand und den übrigen unabhängigen Varia­blen als Regressoren. Toleranzen nahe null deuten auf eine Multikollinearität der unabhängigen Variablen der eigentlichen Regressionsanalyse hin.[2]

		weiblich	männlich
Regression	Regressoren	Toleranz	Toleranz
1.a	GEWTR_1 ABWPOURX REIZBEX1	.963218 .961361 .961361	.914029 .983572 .909303
1.b	GEWTR_1 ABWPOURX REIZBEX1 INVOLV_X	.833641 .940086 .957451 .814981	.784801 .967400 .904410 .765636
2.a	GEWTR_2 KONURS_X RISLUSX1	.972883 .990093 .974331	.956431 .992608 .949542
2.b	GEWTR_2 KONURS_X RISLUSX1 INVOLV_X	.701395 .988905 .962020 .720584	.786629 .991166 .945452 .803569
6.	GEWTR_1 ABWPOURX REIZBEX1	.963218 .993834 .961361	.914029 .983572 .909303

Tab. 2 (Toleranzen)

„Eine exakte Grenze für ‚ernsthafte Multikollinearität‘ läßt sich nicht angeben.“[3] Bei derart hohen Werten, wie sie sich in der oben abgedruckten Übersicht finden, kann eine starke Kollinearität ausgeschlossen werden. Auffällig sind lediglich die Werte des Involvements und die Werte der Gewöhnung, wenn das Involvement mit in die Untersuchung einbezogen wird. Im weiteren wird davon ausgegangen, daß keine Multikollinearität zwischen den unab­hängigen Variablen besteht.

---

[1] vgl.: Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. (1994), S. 33

[2] vgl.: Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. (1994), S. 41

[3] Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. (1994), S. 42

Voraussetzung für die Anwendung von t-Test und F-Test im klassischen Regressionsmodell ist eine Normalverteilung der Residuen. Diese Normalverteilungsannahme ist zur Kleinst-Quadrate-Schätzung der Koeffizienten des linearen Regressionsmodells an sich nicht erforderlich. Wenn diese Annahme jedoch erfüllt ist, ist der Kleinst-Quadrate-Schätzer identisch mit dem Größte-Dichte-Schätzer (=Maximum-Likelihood-Schätzer).[1]

Sowohl Backhaus[2] als auch Kockläuner[3] empfehlen zur Überprüfung der Normalvertei­lungs­an­nahme die Überprüfung anhand von graphischen Hilfsmitteln. Zu diesem Zweck bieten sich vor allem zwei graphische Unterstützungen an. An erster Stelle steht hier das Histogramm der standartisierten Residuenwerte, das über den Regressionsbefehl von SPSS zu erreichen ist. Dabei wird die Verteilung der Residuenwerte einer stilisierten Normalverteilung gegenübergestellt. Auf der anderen Seite stellt SPSS unter dem Regressionsbefehl den Normal Probability (P-P) Plot zur Verfügung. Dieses Diagramm entsteht dadurch, daß die vorliegenden standartisierten Residuenwerte der Größe nach geordnet werden, um auf der vertikalen Achse die zugehörigen Werte ihrer empirischen Verteilungsfunktion abtragen zu können. Auf der horizontalen Achse werden diesen die Funktionswerte der standartisierten Normalverteilung gegenübergestellt. Dies ist die empirische Verteilungsfunktion der Erwartungs­werte von n Ordnungsstatistiken. Letztere ergeben sich aus der größenmäßigen Anordnung von n unabhän­gigen standartisierten normal­verteilten Zufallsvariablen. Prozentpunkte deren Verteilung liefern die angesprochenen Erwartungswerte. Normal Probability Plots sind dann wie folgt zu interpre­tieren: Nach Konstruktion der Achsen sind alle Koordinatenpaare immer dann auf der stilisier­ten Gerade liegend zu erwarten, wenn die eingehenden Beobachtungen Realisationen unabhän­gig standardisierter normalverteilter Zufallsvariablen darstellen.[4]

Grundsätzlich ist davon auszugehen, daß die Normalverteilungsannahme in der Regel verletzt sein wird, weil Normalverteilungen in der Realität kaum vorkommen. Der zentrale Grenz­wertsatz liefert aber die Argumentation dafür, daß die Störgrößen im Regressionsmodell wenigstens als näherungsweise normalverteilt gelten können.[5] In diesem Zusammenhang ist je­doch die Gefahr der Supernormalität zu beachten. Kurz zusammengefaßt ist darunter zu verstehen, daß bei großen Stichproben die Residuenwerte als gewichtete Summe der Störgrö­ßen auch dann annähernd normalverteilt sein können, wenn die Störgrößen nicht einer Normal­verteilung genügen. Daher läßt die Verteilung der Residuen oft nicht die Verletzung der Nor­malverteilungsannahme erkennen. Hinzu kommt in dieser Untersuchung, daß die Konstrukte aus mehreren Items gebildet werden, was die Nicht-Normalität weiter verschleiert. „Trotzdem bleibt diese Verteilung das einzige Instrument zur Überprüfung der Normalverteilungs­annahme, die für alle n Störgrößen ui und damit n einzelne Verteilungen gelten soll.“[6] Auf die weiteren statistischen Bedingungen für die Überprüfung der Normalverteilungsannahme wird an dieser Stelle nicht eingegangen, da diese statistischen Feinheiten nicht Thema einer inhaltlichen Arbeit sein können und den Umfang der Arbeit sprengen würden. Der interessierte Leser sei auf Kockläuner[7] verwiesen. Nur soviel soll hier angemerkt werden: Für die Überprüfung der Normalitätsannahme werden die intern studentisierten Residuen betrachtet, um konstante Varianzen sicherzustellen[8]. Außer­dem sollte die Normalitätsbedingung nach Kockläuner die zuletzt zu überprüfende Bedingung sein. Dies hat den Vorteil, daß nicht von n einzelnen Verteilungen, also für jede einzelne Störgröße eine, ausgegangen werden muß, zu denen jeweils nur ein Residuenwert zur Verfü­gung steht, sondern von einem Verteilungsmodell, zu dessen Überprüfung n Residuenwerte vorliegen.[9]

Die Überprüfung der graphischen Darstellungen führte zu folgenden Ergebnissen: Weitgehend lassen die Normal Probability Plots und vor allem die Histogramme eine relativ gute Anpassung an die Normalverteilung erkennen. Stärkere Abweichungen sind vor allem bei der 3. Regression und männlichem Geschlecht und bei der 5. Regression und weiblichem Geschlecht zu erkennen. Die Graphiken sind nicht in dieser Arbeit abgedruckt, können jedoch mit Hilfe der Syntax auf der beigefügten Diskette problemlos dargestellt werden.

Zur Überprüfung der Residuen auf Normalverteilung, soll zusätzlich der Kolmogorov-Smirnov-Anpassungstest durchgeführt werden. Dieser ist für kleine Stichproben besser geeignet als der 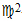-Test, da letzterer nur approximativ arbeitet.[10] Im Falle eines Ablehnens der Normal­verteilungsannahme durch diesen, kann im Anschluß noch eine weitere Verteilungsüberprüfung über Schiefe und Exzeß durchgeführt werden.

Die H0 des Kolmogoroff- Smirnov-Anpassungstest lautet, daß die empirisch ermittelte Vertei­lung gleich der Normalverteilung ist. Die Alternativhypothese lautet, daß sich die beiden Verteilungen für mindestens einen Wert der unabhängigen Variable unterscheiden. Die Hypo­these H0 wird nun zum Niveau 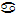verworfen, wenn Dn multipliziert mit der Wurzel aus der Anzahl der Beobachtungen, größer oder gleich dem aus der Tabelle[11] zu entnehmenden kritischen Wert ist. „Die Größe Dn gibt den größten vertikalen Abstand zwischen hypothetischer und empirischer Verteilungsfunktion an.“[12] Nun ist das Signifikanzniveau zu bestimmen. Üblicherweise wird ein Signifikanzniveau von 1% oder 5% gewählt. An dieser Stelle ist zu beachten, daß es hier darum geht, die Normalverteilungsannahme zu überprüfen und dabei den 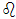-Fehler, das heißt eine fälschliche Beibehaltung der Nullhypothese zu minimieren. Da sich der 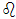-Fehler aus 1- 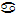-Fehler berechnet, erscheint es sinnvoll, das Signifikanzniveau an dieser Stelle höher anzusetzen. Im Rahmen der dieser Arbeit wird deshalb ein Signifikanzniveau von 10% zur Ablehnung der Normalverteilungsannahme angesetzt.

 

	weiblich		männlich
Regression	K-S-z	Signif.-Ni­veau	K-S-z	Signif.-Ni­veau
1.a	1.1021	.1761	0.8518	.4626
1.b	0.4965	.9662	0.6876	.7317
2.a	0.8341	.4898	1.0320	.2373
2.b	1.0907	.1851	0.7863	.5666
3.	1.0867	.1884	1.1211	.1618
4.	0.7999	.5444	0.7258	.6680
5.	1.0018	.2681	0.6126	.8472
6.	0.9536	.3230	0.7569	.6156

Tab. 3 (Kolmogoroff-Smirnov-Test-Wert)

Für sämtliche Regressionen liegen die Kolmogoroff-Smirnov-z-Prüfgrößen und die entspre­chenden Signifikanzniveaus über dem geforderten Mindestmaß[13]. Kritisch sind vor allem die Kolmogoroff-Smirnov-z-Prüfgrößen für die Regression 1.a (weiblich), die Regression 5. (weiblich), da hier ja nur 38 Werte in die Untersuchung eingehen und Regression 3. (männlich). Die Normalverteilungsannahme für die Residuenwerte wird trotzdem für alle Regressionen als bestätigt angesehen. Auch das dritte und fünfte Regressionsmodell werden weiter verfolgt, auch wenn vor allem bei dem dritten Modell die Werte auf eine schlechte Erfüllung der Nor­malverteilungsannahme hindeuten.

---

[1] vgl.: Gruber, Josef, (1982), S. 58

[2] vgl.: Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R., (1994), S. 32

[3] vgl: Kockläuner, Gerhard, (1988), S. 58 ff

[4] vgl.: Kockläuner, Gerhard, (1988), S. 58 ff

[5] vgl.: Hartung, J., (1982), S. 122

[6] Kockläuner, Gerhard, (1988), S. 73

[7] Kockläuner, Gerhard, (1988), S. 60-76

[8] vgl.: Kockläuner, Gerhard, (1988), S. 63

[9] Kockläuner, Gerhard, (1988), S. 73

[10] vgl.: Hartung, J., (1982), S. 183

[11] vgl.: Hartung; J. (1982), S. 184

[12] Hartung; J. (1982), S. 184

[13] vgl.: Hartung; J. (1982), S. 184

Nachdem die Prämissen des linearen Regressionsmodells weitgehend gesichert sind, muß nun der Zusammenhang zwischen Regressoren und Regressand näher untersucht werden.

An erster Stelle wird nun überprüft, ob die Regressoren insgesamt überhaupt einen Einfluß auf den Regressanden haben. Dabei wird die Nullhypothese, die besagt, daß die Regressions­funktion als ganzes unbrauchbar ist, gegen die Alternativhypothese, daß die Regressoren einen Einfluß auf den Regressanden haben, getestet. Als Signifikanzniveau wird hier .99 festgelegt. Dadurch wird erreicht, daß eine Ablehnung der Nullhypothese mit 99 %-iger Wahrschein­lichkeit nicht zu unrecht erfolgt.

In der folgenden Tabelle sind für beide Geschlechter jeweils in der ersten Spalte, der Anteil der durch die Regressoren erklärte Streuung, bereinigt um die Einflüsse durch die Anzahl der Regressoren wiedergegeben. In den darauf folgenden Spalten sind zuerst der F-Wert und danach das dazu gehörige Signifikanzniveau dargestellt.

		weiblich			männlich
Regression	Adjusted R Square	F	Signif F	Adjusted R Square	F	Signif F
1.a	.11899	5.63696	.0013	.18846	9.05052	.0000
1.b	.41877	19.55244	.0000	.32525	13.53285	.0000
2.a	.29286	15.21892	.0000	.26307	13.37552	.0000
2.b	.29092	11.56449	.0000	.28397	11.31143	.0000
3.	.26416	37.97533	.0000	.06655	8.41488	.0046
4.	.43459	27.67024	.0000	.20778	13.85188	.0005
5.	.13298	6.67470	.0140	.01627	1.81021	.1848
6.	.34825	19.34569	.0000	.34989	19.65775	.0000

Tab. 4 (Bestimmtheitsmaß und F-Test)

Besonders ins Auge fallen die Ergebnisse bezüglich der Regressionen 1.a, 3. und 5.. Da die Ergebnisse der 5. Regression sowohl bezüglich des Bestimmtheitsmaßes, als auch bezüglich des Signifikanzniveaus nicht befriedigend sind, soll diese Regression aus der weiteren Analyse ausgeschlossen werden. Aufgrund der Daten in der Stichprobe muß davon ausgegan­gen werden, daß die Regressoren in der 5. Regression keinen Einfluß auf den Regressanden haben. Die Ergebnisse der 1. und 3. Regression sollen weiter untersucht werden, um unter Umständen später eine Erklärung, vor allem für die niedrigen Werte des Bestimmtheitsmaßes zu finden. Auffällig ist, daß vor allem die Regressionen, die schlechte Werte bei der Überprüfung der Normalverteilungsannahme zeigten, auch beim F-Test schlechte Werte zeigen. Wie schon vorher angemerkt wurde, führt eine Verletzung der Normalverteilungsannahme nicht dazu, daß die Kleinst-Quadrate-Regression nicht effizient ist, sondern nur dazu, daß F-Test und t-Test weniger aussagekräftig sind. Aus diesem Grunde werden die Ergebnisse bei Regression 1. und Regression 3. toleriert.

Nachdem bestätigt ist, daß die Regressoren insgesamt einen Einfluß auf den Regressanden haben, bleibt nun zu überprüfen, wie der Einfluß der einzelnen Regressoren einzuschätzen ist und ob die Richtung des Einflusses mit den Hypothesen übereinstimmt.

			weiblich			männlich
Re­gres­sion	Regressoren	Beta	T	Sig T	Beta	T	Sig T
1.a	GEWTR_1 ABWPOURX REIZBEX1	.290050 -.255284 -.008455	3.078 -2.752 -.090	.0027 .0070 .9288	.405656 -.178608 -.071942	4.390 -2.005 -.777	.0000 .0476 .4392
1.b	GEWTR_1 ABWPOURX REIZBEX1 INVOLV_X	.071241 -.124639 .027043 -.603364	.866 -1.609 .352 -7.251	.3886 .1109 .7254 .0000	.212831 -.129943 -.043150 -.426594	2.265 -1.587 -.509 -4.634	.0257 .1157 .6116 .0000
2.a	GEWTR_2 KONURS_X RISLUSX1	-.561661 .110919 .134159	-6.686 1.332 1.598	.0000 .1859 .1131	-.524450 .086420 -.005601	-6.0931 .023 -.065	.0000 .3088 .9484
2.b	GEWTR_2 KONURS_X RISLUSX1 INVOLV_X	-.527141 .095841 .144335 .081043	-5.646 1.124 1.700 .852	.0000 .2636 .0923 .3962	-.418910 .029124 -.021382 .202651	-4.185 .330 -.250 1.987	.0001 .7417 .8031 .0497
3.	SUMAFF_X	-.520865	-6.162	.0000	-.274823	-2.901	.0046
4.	SUMAFF_X	-.659232	-5.260	.0000	-.473236	-3.722	.0005
6.	GEWTR_1 ABWPOURX REIZBEX1	.514688 .076574 -.228024	6.350 .960 -2.811	.0000 .3395 .0059	.539957 -.153865 -.101771	6.529 -1.277 -1.856	.0000 .2047 .0664

Tab. 5 (Regressionskoeffizient und t-Test)

In der obigen Tabelle, sind getrennt nach Geschlecht für jeden Regressor in jeder Regression die standardisierten Koeffizienten, die T-Werte und die entsprechenden Signifikanzniveaus angege­ben. Auf die Konfidenzintervalle wird nicht näher eingegangen werden. In der Tabelle sind lediglich die Koeffizienten, bei denen die Konfidenzintervalle besonders gering sind, markiert.

Die Ergebnisse des T-Test werden im folgenden Kapitel interpretiert.