Formale Analyse

Zum besseren Verständnis der folgenden Auswertung sei die Orientierung der Variablen in der folgenden Übersicht kurz zusammengefaßt.

Variable	Bedeutung hoher numerischer Werte	Bedeutung niedriger numerischer Werte
ABWAFF2X	groß (positiv)	klein (negativ)
GEWOEH_X	klein	groß
RISIKO2X	klein (positiv)	groß (negativ)
ABWPOURX	klein	groß
INVOLV_X	klein	groß
KONURS_X	klein	groß
GESAFF_X	klein (negativ)	groß (positiv)
SUMAFF_X	groß (positiv)	klein (negativ)
WKW_X	klein	groß
REIZBEX1	klein	groß
RISLUSX1	klein	groß

Tab. 6 (Orientierung der Variablen)

Durch die Regression 1.a werden drei der aufgestellten Hypothesen bestätigt. Erstens wird bestätigt, daß ein negativer Zusammenhang zwischen der Gewöhnung und dem Abwechslungs­affekt besteht (1. Hypothese) und zweitens, daß dieser Zusammenhang durch eine logarithmi­sche Kurve dargestellt werden kann (2. Hypothese). Die Ergebnisse für diesen Zusammenhang bewegen sich für beide Geschlechter auf einem Signifikanzniveau größer als 99%. Drittens konnte durch diese Regression nachgewiesen werden, daß ein positiver Zusammenhang zwi­schen dem ursprünglichen Abwechslungspotential und dem aktuellen Abwechslungsaffekt besteht (8. Hypothese). Das Signifikanzniveau liegt für beide Geschlechter über 95 %. Nicht abgelehnt werden kann aufgrund dieser Regression die Nullhypothese, die besagt, daß kein Zusammenhang zwischen dem Reizbedürfnis und dem Abwechslungsaffekt besteht (10. Hypothese). Das Si­gnifikanzniveau liegt bei den Männern unter 60% und bei den Frauen sogar unter 10%. Somit ist davon auszugehen, daß hier kein Zusammenhang besteht. Darüber hinaus weisen die Koef­fizienten der Variable REIZBEX1 nicht die vorhergesagte Orientierung auf.

Die Regression 1.b ist in erster Linie durchgeführt worden, um zu untersuchen, ob die Variable Involvement einen Beitrag zur Erklärung der Varianz leisten kann. Ein dermaßen starker Einfluß, wie er in Regression 1.b zu erkennen ist, kann durch die bisher erläuterten theoreti­schen Zusammenhänge nicht erklärt werden. Durch die Einbeziehung des Involvements sinken zum einen die Signifikanzniveaus der übrigen Regressoren und zum anderen ist an dem stan­dardisierten Koeffizienten eine überragende Bedeutung dieses Regressors zu erkennen.

Die Regression 2.a bestätigt die Hypothese, daß der Risikoaffekt umso negativer ist, je geringer die Gewöhnung ist (3. Hypothese). Für beide Geschlechter liegt das Signifikanzniveau über 99,99%. Außerdem ist das Konfidenzintervall verhältnismäßig gering. Obwohl, wie schon erläutert, die mathematischen Vorgaben durch die Transformation nicht komplett erfüllt wurden, wird durch diese Regression die 4. Hypothese bestätigt, da GEWTR_2 die quadrierte Variable GEWOEH_X ist. Zwar stimmt die Orientierung der Koeffizienten der Variable für das ursprünglichen Risikopotential, die Signifikanzniveaus deuten mit ca. 82% für die Frauen und ca. 70% für die Männer eher auf einen zufälligen Zusammenhang hin. Damit ist die 7. Hypothese abzulehnen. Auch bei der Risikotoleranz lassen die Signifikanzwerte keine Ableh­nung der Nullhypothese zu. Bei den Frauen, bei denen das Signifikanzniveau immerhin bei ca. 89% liegt, ist zudem eine der 9. Hypothese zuwiderlaufende Orientierung zu beobachten.

Die Einführung der Variablen Involvement in der Regression 2.b trägt kaum zur Erklärung der Varianz bei. Auch für diesen großen Unterschied zwischen Regression 1.b und 2.b in bezug auf den Einfluß der Variable Involvement, liefert die Theorie keine Erklärung. Die Frage ist, warum der Einfluß im Zusammenhang mit dem Abwechslungsaffekt so groß und beim Risiko­affekt so gering ist. Interessant ist die Beobachtung, daß sich der standardisierte Koeffizient der Gewöhnung gegenüber der Regression 2.a kaum verändert und auch wieder ein relativ enges Konfidenzintervall besitzt.

Die Regression 3. kann eindeutig die 5. Hypothese bestätigen, daß der empfundene Gesamtaf­fekt mit steigender Summe der beiden Einzelaffekte steigt. Beide Geschlechter zeigen ein Signi­fikanzniveau von über 99%. Ob der geringe Wert des Bestimmtheitsmaßes bei den Männern mit ca. 7% ein Artefakt ist oder eine theoretische Fundierung hat, bleibt hier ungeklärt. Insgesamt sollte aber gerade diese Regression mit Vorsicht interpretiert werden, da sie schon bezüglich der Normalverteilungsannahme und des F-Testes sehr schlechte Ergebnisse geliefert hat. Darüber hinaus traten zum einen bei der Validitätsüberprüfung des Konstruktes GESAFF_X erhebliche Fehlladungen auf, zum anderen ist die Reliabilität von GESAFF_X nicht vorbehaltslos gesi­chert.

Die Regression 4. trifft nicht genau die 6. Hypothese. Da jedoch die 5. Regression, die diese Hypothese bestätigen sollte, nicht weiter verfolgt wurde, kann die 4. Regression zumindest aufzeigen, daß ein Zusammenhang zwischen diesen beiden Affekten und der Wiederkaufwahrscheinlichkeit besteht. Es sollte dabei nicht übersehen werden, daß noch viele andere Faktoren bei der Wiederkaufwahrscheinlichkeit eine Rolle spielen können. Die extrinsi­schen Motivationen wurden teilweise ausgeschaltet, indem EXTRI_3 gleich 1 herausgefiltert wurde. Die Ergebnisse sind hochsignifikant mit einer Wahrscheinlichkeit von über 99% bei beiden Geschlechtern.

In der folgenden Tabelle sind die Entscheidungen bezüglich der Hypothesen 1 bis 10 über­sichtsartig zusammengefaßt.

Hypothese	Entscheidung
1. Hypothese	Bestätigung
2. Hypothese	Bestätigung
3. Hypothese	Bestätigung
4. Hypothese	Bestätigung
5. Hypothese	Bestätigung
6. Hypothese	Bestätigung unter Vorbehalt
7. Hypothese	Beibehaltung der Ho
8. Hypothese	Bestätigung
9. Hypothese	Beibehaltung der Ho
10. Hypothese	Beibehaltung der Ho

Tab. 7 (Ergebniszusammenfassung)

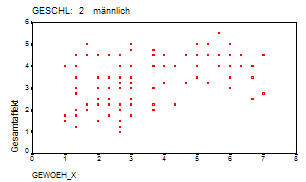
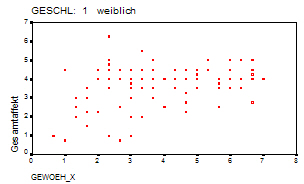
Damit sind alle Hypothesen bis auf die 11. Hypothese behandelt. Die 6. Regression hat den Zweck, sich an 11. Hypothese anzunähern. Das Scatterplot des Gesamtaffektes in bezug auf die Erregung läßt keinen kurvili­nearen Zusammenhang erkennen. (siehe Abb. 11a und Abb. 11b) Dies war auch nicht zu erwarten, da schon alleine die Einflußfaktoren auf die Einzelaffekte, zu einer Verzerrung führen. Dabei sind dann mögliche andere Einfluß­faktoren auf den Ge­samtaffekt noch nicht berücksichtigt. Um der Bestäti­gung der Hypothese ein wenig näher zu kommen, wurde des­halb folgender Weg eingeschlagen. Der Gesamtaffekt wurde um den Risikoaffekt und damit auch um alle diesen beeinflussenden Faktoren be­reinigt. Damit enthält der verbleibende Affekt annahmegemäß nur noch den Abwechslungsaffekt und die diesen beeinflussenden Faktoren, wenn von möglichen anderen Affekten abstra­hiert wird. Die Regression mit den Faktoren des Abwechslungsaffektes bringt erwartungsgemäß eine hohe Erklärung der Varianz, die bei Männern und Frauen ähnlich ist und mit etwa 35% sogar noch über dem Bestimmtheitsmaß der Regression 1.a mit 12% für Frauen und 19% für Männer liegt. Wenn zu der Varianzerklärung in der 6. Regression die Varianzaufklärung in der Regression 2.a gerechnet wird, dann werden hier Werte um 60% erreicht. Dies deutet darauf hin, daß der Gesamtaffekt in erster Linie durch die dargestellten Faktoren bedingt wird. In der 6. Regression konnten, mit einem Signifikanzniveau von über 99,99% und einem vergleichsweise engen Konfidenzintervall, gute Ergebnisse für den Regressor Gewöhnung erreicht werden. Dabei sind die ermittelten Koeffizienten für die Gewöhnung für beide Geschlechter in etwa gleich. Die Ergebnisse für das ursprüngliche Abwechslungspotential sind nicht signifikant. Die Ergebnisse für das Reizbedürfnis sind zwar auf einem Niveau von 99% für Frauen und 93% für Männer signifikant, die Koeffizienten haben jedoch nicht das vorhergesagte Vorzeichen.

Die 6. Regression wurde zusätzlich in einer modifizierten Weise durchgeführt, indem aus dem Gesamtaffekt nicht der Risikoaffekt herausgerechnet wurde, sondern statt dessen der Abwechs­lungsaffekt. Das Ergebnis der anschließenden Regression, vor allem die Varianzaufdeckung, war jedoch nicht sehr erfolgreich. Dies ist vermutlich in erster Linie darauf zurückzuführen, daß es bei dem Risikoaffekt nicht so gut wie bei dem Abwechslungsaffekt gelungen ist, eine Skalen­transformation vorzunehmen. So gleicht der Graph des Abwechslungsaffektes recht gut der Logarithmuskurve, während die Annäherung der Risikoaffektkurve durch die Kurve zweiten Grades nicht so gut gelungen ist. Darüber hinaus könnten die Validitätsprobleme des Konstruk­tes Konsequenzen eine Rolle spielen.